树的定义

树是n(n>=0)个结点的有限集。n=0 时称为空树。

结点的分类

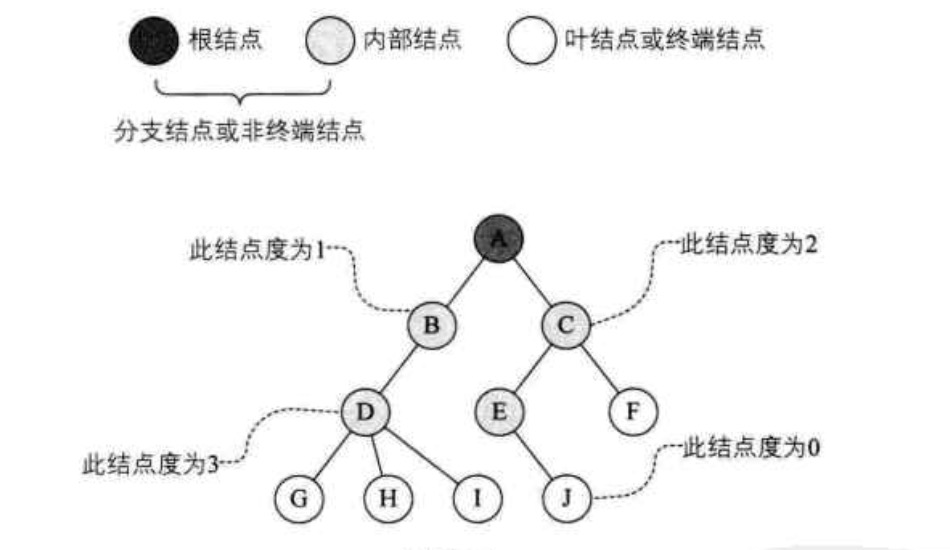
结点拥有的子树数称为结点的度(Degree)。度为 0 的结点称为叶结点(Leaf)或者终端结点；度不为 0 的结点称为非终端结点或者分支结点。除根结点之外，分支结点也称为内部结点。树的度是树内各结点的度的最大值。

如下图，因为这棵树结点的度的最大值是结点 D 的度，为 3，所以树的度也为 3。

树的存储结构

有双亲表示法、孩子表示法、孩子兄弟表示法 3 种表示法表示树的结构。

双亲表示法

data	parent

其中，data 是数据域，存储结点的数据信息；而 parent 是指针域，存储该结点的双亲在数组中的下标。以上数据结构可拓展，比如加入个孩子结点域firstchild或者加个右兄弟域rightsib。

#define MAX_TREE_SIZE 100

typedef int TElemType;

typedef struct PTNode
{
    TElemType data; //结点数据域
    int parent;     //双亲位置
}PTNode;

typedef struct      //树结构
{
    PTNode nodes[MAX_TREE_SIZE];    //结点数组
    int r, n;       //根的位置和结点数
} PTree;

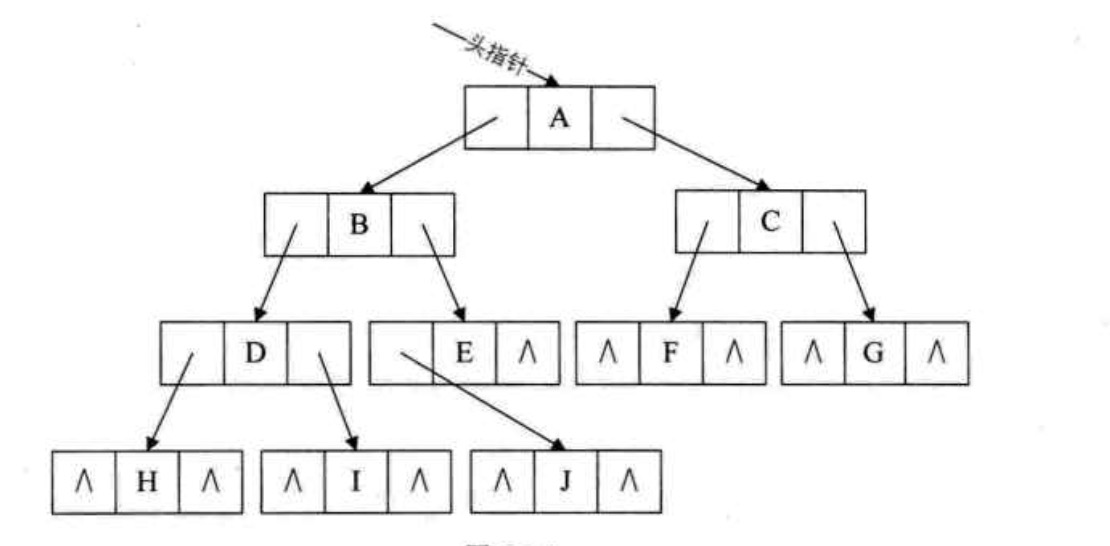
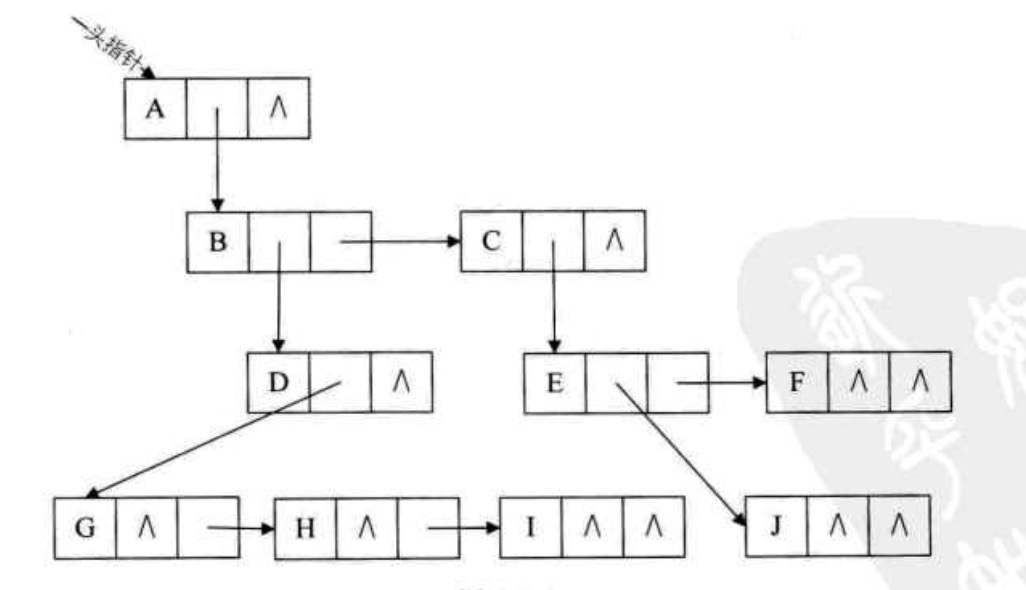
孩子表示法

把每个结点的孩子结点排列起来，以单链表做存储结构，则 n 个结点有 n 个孩子链表，如果是叶子结点则此单链表为空。然后 n 个头指针又组成一个线性表，采用顺序存储结构，存放进一个一维数组中。

如下：

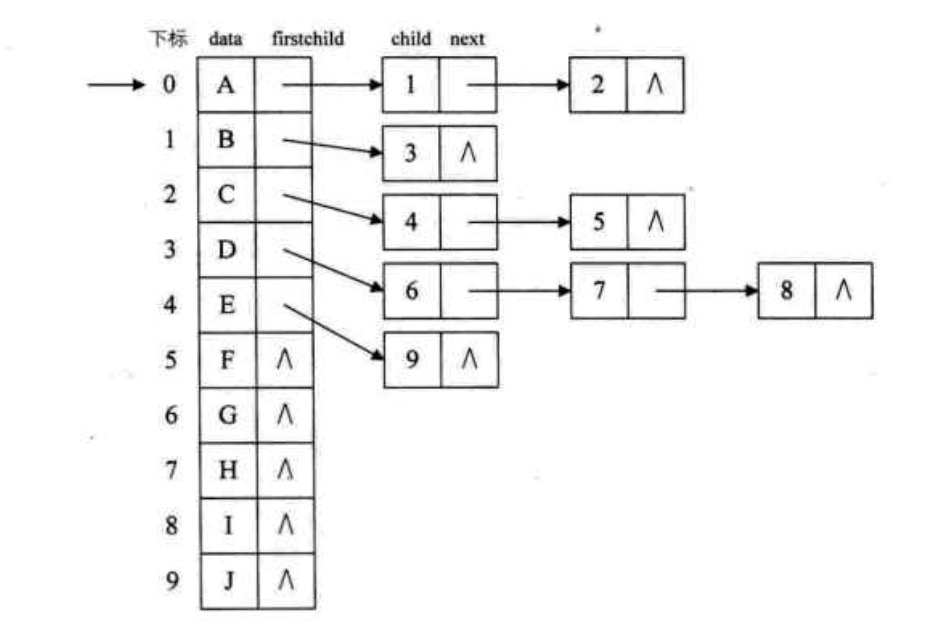
为此，设计两种结点结构，一个是孩子链表的孩子结点。

child	next

其中 child 是数据域，用来存储某个结点在表头数组中的下标。next 是指针域，用来存储指向某个结点的下一个孩子结点的指针。

另一个是表头数组的表头结点，如下：

data	firstchild

其中 data 是数据域，存储某结点的数据信息。firstchild 是头指针域，存储该结点的孩子链表的头指针。

以下是孩子表示法的结构定义：

/*数的孩子表示法结构定义*/
#define MAX_TREE_SIZE 100

typedef int TElemType;

typedef struct CTNode //孩子结点
{
    int child;
    struct CTNode *next;
} *ChildPtr;

typedef  struct //表头结构
{
    TElemType data;
    ChildPtr firstchild;
}CTBox;

typedef struct //树结构
{
    CTBox nodes[MAX_TREE_SIZE]; //结点数组
    int r, n;   //根的位置和结点树
}CTree;

这样的结构对于我们要查找某个结点的某个孩子，或者找某个结点的兄弟，只需要查找这个结点的孩子单链表即可。对于遍历整棵树也是很方便的，对头结点的数组循环即可。

但是，如果要寻找某个结点的双亲是谁就会比较麻烦，需要遍历整棵树才行。这时候稍微改下设计就好了，添加个父结点域。如下：

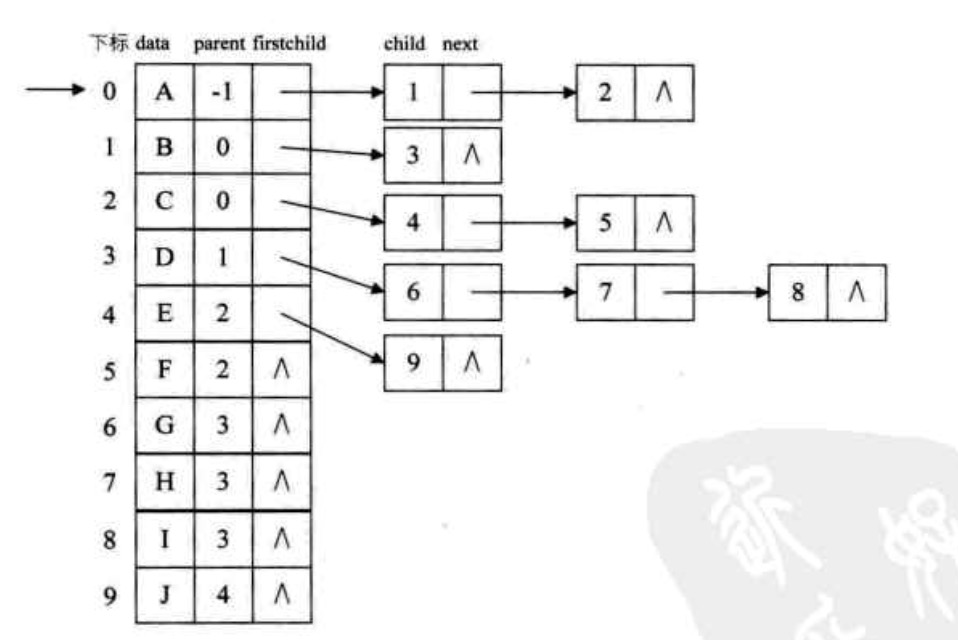
孩子兄弟表示法

结点结构设计如下：

data	firstchild	rightsib

其中 data 是数据域，firstchild 为指针域，存储该结点的第一个孩子结点的存储地址，rightsib 是指针域，存储该结点的右兄弟结点的存储地址。

结构定义代码如下：

#define MAX_TREE_SIZE 100

typedef int TElemType;

typedef struct CSNode
{
    TElemType data;
    struct CSNode *firstchild, *rightsib;
} CSNode, *CSTree;

二叉树

二叉树（Binary Tree）是 n(n>=0)个结点的有限集合，改集合或者为空集（称为空二叉树）,或者由一个根结点和两颗互不相交的、分别称为根节点的左子树和右子树的二叉树组成。

二叉树具有五种基本形态：

空二叉树
只有一个根结点
根结点只有左子树
根结点只有右子树
根结点既有左子树又有右子树

特殊二叉树

斜树

所有结点都只有左子树的二叉树叫左斜树；所有结点都只有右子树的二叉树叫右斜树。这两者统称为斜树。

满二叉树

在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子都在同一层上，这样的二叉树称为满二叉树。

完全二叉树

对一棵具有 n 个结点的二叉树按层序编号，如果编号为 i（1<=i<=n）的结点与同样深度的满二叉树中编号为 i 的结点在二叉树中位置完全相同，则这棵二叉树称为完全二叉树。

二叉树性质

存储结构

其中，data 是数据域，lchild 和 rchild 是指针域，分别存放指向左孩子和右孩子的指针。

typedef int TElemType;

/*二叉树的二叉链表结点结构定义*/
typedef struct BiTNode  //结点结构
{
    TElemType data;
    struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;