选择排序

原理

选择排序很简单，步骤如下：

首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置
然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾
以此类推，直到所有元素均排序完毕。

之所以称之为选择排序，是因为每一次遍历未排序的序列我们总是从中选择出最小的元素。

下面是选择排序的动画演示

实现

void selection_sort(int arr[], int len) {
	int i, j, min, temp;
	for (i = 0; i < len - 1; i++) {
		min = i;
		for (j = i + 1; j < len; j++)
			if (arr[min] > arr[j])
				min = j;
	   	temp = arr[min];
		arr[min] = arr[i];
		arr[i] = temp;
	}
}

分析

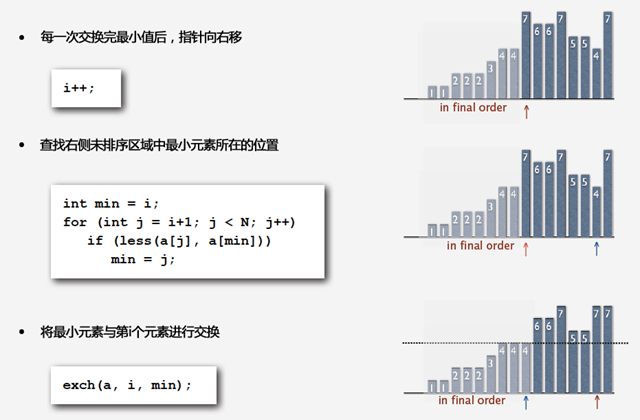
下图分析了选择排序中每一次排序的过程，您可以对照图中右边的柱状图来看。

时间复杂度

选择排序的交换操作介于0和(n-1)次之间。选择排序的比较操作为n(n-1)/2次之间。选择排序的赋值操作介于0和3(n-1)次之间。

比较次数O(n^2)，比较次数与关键字的初始状态无关，总的比较次数 N=(n-1)+(n-2)+...+1=n(n-1)/2。交换次数O(n)，最好情况是，已经有序，交换0次；最坏情况是，逆序，交换n-1`次。交换次数比冒泡排序较少，由于交换所需CPU时间比比较所需的CPU时间多，n值较小时，选择排序比冒泡排序快。

原地操作几乎是选择排序的唯一优点，当空间复杂度要求较高时，可以考虑选择排序；实际适用的场合非常罕见。

冒泡排序

原理

冒泡排序是一种简单的排序算法，步骤如下：

比较相邻的元素。如果第一个比第二个大，就交换他们两个。
对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
针对所有的元素重复以上的步骤，除了最后一个。
持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较

冒泡排序对 n 个项目需要O(n^2)的比较次数，且可以原地排序。尽管这个算法是最简单了解和实现的排序算法之一，但它对于包含大量的元素的数列排序是很没有效率的。

实现

#include <stdio.h>
void bubble_sort(int arr[], int len) {
	int i, j, temp;
	for (i = 0; i < len - 1; i++)
		for (j = 0; j < len - 1 - i; j++)
			if (arr[j] > arr[j + 1]) {
				temp = arr[j];
				arr[j] = arr[j + 1];
				arr[j + 1] = temp;
			}
}

int main() {
	int arr[] = { 22, 34, 3, 32, 82, 55, 89, 50, 37, 5, 64, 35, 9, 70 };
	int len = (int) sizeof(arr) / sizeof(*arr);
	bubble_sort(arr, len);
	int i;
	for (i = 0; i < len; i++)
		printf("%d ", arr[i]);
	return 0;
}

分析

最坏时间复杂度 O(n^2)
最优时间复杂度 O(n)
平均时间复杂度 O(n^2)
空间复杂度总共 O(n)，需要辅助空间 O(1)

插入排序

原理

插入排序也是一种比较直观的排序方式。可以以我们平常打扑克牌为例来说明，假设我们那在手上的牌都是排好序的，那么插入排序可以理解为我们每一次将摸到的牌，和手中的牌从左到右依次进行对比，如果找到合适的位置则直接插入。具体步骤：

从第一个元素开始，该元素可以认为已经被排序
取出下一个元素，在已经排序的元素序列中从后向前扫描
如果该元素小于前面的元素（已排序），则依次与前面元素进行比较如果小于则交换，直到找到大于该元素的就则停止；
如果该元素大于前面的元素（已排序），则重复步骤2
重复步骤2~4 直到所有元素都排好序。

下面是插入排序的动画演示:

实现

/// <summary>
/// 插入排序
/// </summary>
/// <param name="array"></param>
public static void InsertionSort(T[] array)
{
    int n = array.Length;
    //从第二个元素开始
    for (int i = 1; i < n; i++)
    {
        //从第i个元素开始，一次和前面已经排好序的i-1个元素比较，如果小于，则交换
        for (int j = i; j > 0; j--)
        {
            if (array[j].CompareTo(array[j - 1]) < 0)
            {
                Swap(array, j, j - 1);
            }
            else//如果大于，则不用继续往前比较了，因为前面的元素已经排好序。
                break;
        }
    }
}

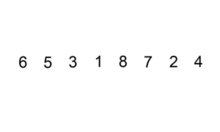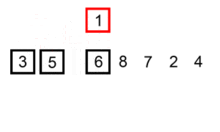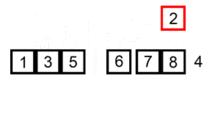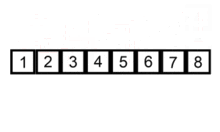
分析

插入排序在各种初始化条件下的排序效果如下：

时间复杂度

最好情况下,排序前对象已经按照要求的有序。比较次数(KCN):n−1 ; 移动次数(RMN):为0。则对应的时间复杂度为O(n)。
最坏情况下,排序前对象为要求的顺序的反序。第i趟时第i个对象必须与前面i个对象都做排序码比较,并且每做1次比较就要做1次数据移动（具体可以从下面给出的代码中看出）。比较次数(KCN):1+2+…+(n-1) = n^2/2 ; 移动次数(RMN):为1+2+…+(n-1) = n^2/2。则对应的时间复杂度为O(n^2)。
如果排序记录是随机的，那么根据概率相同的原则，在平均情况下的排序码比较次数和对象移动次数约为n^2/4，因此，直接插入排序的时间复杂度为O(n^2)。

#快速排序

原理

快速排序使用分治法策略来把一个序列（list）分为两个子序列（sub-lists）。

步骤为：

从数列中挑出一个元素，称为”基准”（pivot），
重新排序数列，所有比基准值小的元素摆放在基准前面，所有比基准值大的元素摆在基准后面（相同的数可以到任一边）。在这个分区结束之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
递归地（recursively）把小于基准值元素的子数列和大于基准值元素的子数列排序。

递归到最底部时，数列的大小是零或一，也就是已经排序好了。这个算法一定会结束，因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去。

这里找到了YouTube上的一个动画演示效果，先看一下然后再来看代码：

实现：

//快速排序
void sort(int *a, int left, int right)
{
    if(left >= right)/*如果左边索引大于或者等于右边的索引就代表已经整理完成一个组了*/
    {
        return ;
    }
    int i = left;
    int j = right;
    int key = a[left];
    
    while(i < j)                               /*控制在当组内寻找一遍*/
    {
        while(i < j && key <= a[j])
        /*而寻找结束的条件就是，1，找到一个小于或者大于key的数（大于或小于取决于你想升
         序还是降序）2，没有符合条件1的，并且i与j的大小没有反转*/
        {
            j--;/*从右向前寻找*/
        }
        
        a[i] = a[j];
        /*找到一个这样的数后就把它赋给前面的被拿走的i的值（如果第一次循环且key是
         a[left]，那么就是给key）*/
        
        while(i < j && key >= a[i])
        /*这是i在当组内从左向前寻找，同上，不过注意与key的大小关系停止循环和上面相反，
         因为排序思想是把数往两边扔，所以左右两边的数大小与key的关系相反*/
        {
            i++;
        }
        
        a[j] = a[i];
    }
    
    a[i] = key;/*当在当组内找完一遍以后就把中间数key回归*/
    sort(a, left, i - 1);/*最后用同样的方式对分出来的左边的小组进行同上的做法*/
    sort(a, i + 1, right);/*用同样的方式对分出来的右边的小组进行同上的做法*/
    /*当然最后可能会出现很多分左右，直到每一组的i = j 为止*/
}

int main(int argc, const char * argv[]) {
    @autoreleasepool {
        
        int arr[] = {2, 5, 1, 0, 3};
        int len = (int)sizeof(arr)/sizeof(*arr);
        sort(arr, 0, len-1);
        
        for (int z = 0; z < len; z++) {
            printf("%d ",arr[z]);
        }
        printf("\n");
    }
    return 0;
}

分析

最坏时间复杂度 O(n^2)

最优时间复杂度 O(nlog n)

平均时间复杂度 O(nlog n)

归并排序

原理

归并排序也是采用分治法的思想。

递归法

将序列每相邻两个数字进行归并操作，形成 floor(n/2) 个序列，排序后每个序列包含两个元素
将上述序列再次归并，形成 floor(n/4) 个序列，每个序列包含四个元素
重复步骤2，直到所有元素排序完毕

动画解释：

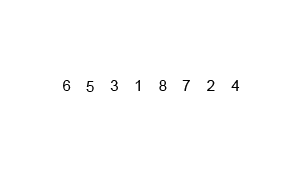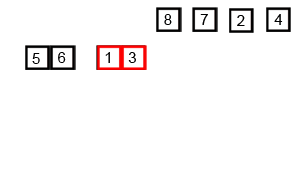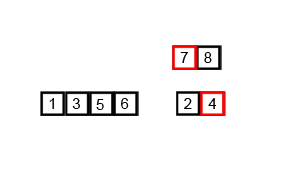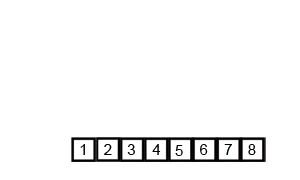
实现

void merge_sort_recursive(int arr[], int reg[], int start, int end) {
    if (start >= end)
        return;
    int len = end - start, mid = (len >> 1) + start;
    int start1 = start, end1 = mid;
    int start2 = mid + 1, end2 = end;
    merge_sort_recursive(arr, reg, start1, end1);
    merge_sort_recursive(arr, reg, start2, end2);
    int k = start;
    while (start1 <= end1 && start2 <= end2)
        reg[k++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];
    while (start1 <= end1)
        reg[k++] = arr[start1++];
    while (start2 <= end2)
        reg[k++] = arr[start2++];
    for (k = start; k <= end; k++)
        arr[k] = reg[k];
}
void merge_sort(int arr[], const int len) {
    int reg[len];
    merge_sort_recursive(arr, reg, 0, len - 1);
    
    for (int z = 0; z < len; z++) {
        printf("%d ",reg[z]);
    }
    printf("\n");
}

int main(int argc, const char * argv[]) {
    @autoreleasepool {
        
        int arr[] = {2, 5, 1, 0, 3};
        int len = (int)sizeof(arr)/sizeof(*arr);
        
        merge_sort(arr,len);
        
    }
    return 0;
}

分析